Jo Niemeyer
“Golden mean spirals”
Original Graphics, signed and numbered, 2006/7.

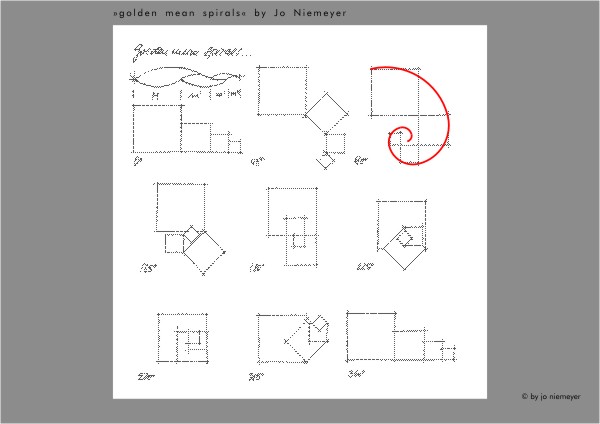
How variously and vividly the golden section can be shown is demonstrated in
this graphic arts series executed in 2006. Four squares following on each other,
whose side lengths comparatively decrease by the golden section, are agilely
connected on the corners. The relative twist corner between two squares following
on each other is steady. In a series of eight graphics the respective stations
are shown in steps of 45°.
“Golden mean spirals” - detail
Jo Niemeyer, artist
"Art and mathematics… an experiment... The basis of my work as an artist is the connection between art and nature, between the artistic action and the experimental work. This means that my artistic production which is fundamentally based on natural principles and measures is nothing more than a sequence of experimental steps which implies given and objective criteria and subjective factors in the same way. On the one hand my work is based on events in nature and civilization as well as on communication with colleagues of other disciplines. The dual pole mathematics - art is for me not only the basis of my experience but at the same time my central theme. My main interest is directed to the perception of space, time, distances and proportion and forms the synthesis between art and nature which implies in the end a dialogue between man and nature..."
http://www.math.unibas.ch/~walser/Arbeiten_mit_weiteren_Autoren/Niemeyer_Walser/Goldener_Schnitt.pdf (link)
http://www.partanen.de/271.html (link for java applet)
http://www.jo.niemeyer.com (link to Jo's homepage)
Another work by the artist
“golden section construction 271...”
Prints + 1 original, 20" x 24", 2007.

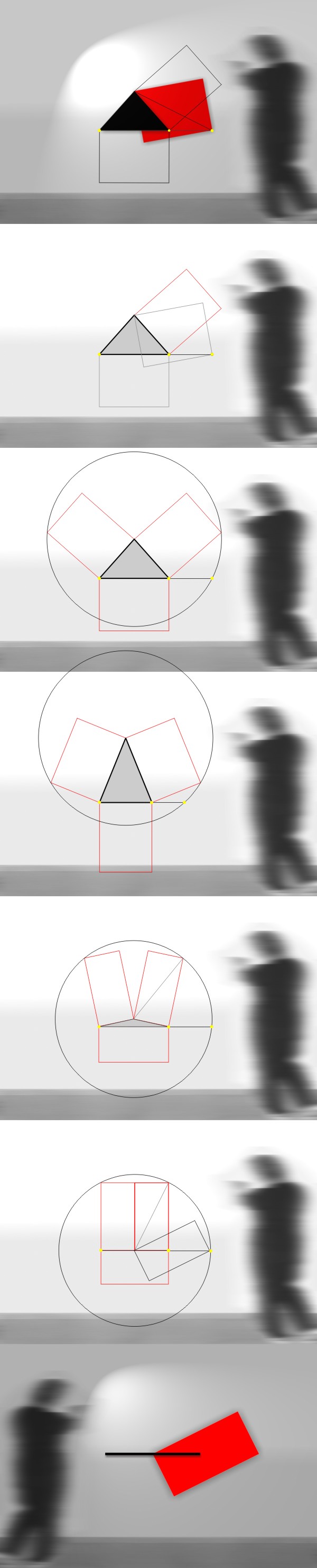
W hen an isosceles triangle of any height is constructed on a line segment, we obtain according to our drawing an extension of the golden section via the diagonal of the rectangle with sides corresponding to two different sides of the triangle.
As we have a free variable we obtain an infinite number of possible constructions for the golden section.
On the last sheet the triangle is 'degenerated' to a line and a centre and corresponds to the customary classical construction.
Conclusion: When we construct a triangle using three congruent rectangles of any size, we obtain according to our drawing the extension of the golden section. This also works the upright way, reversing the sides!