Michael Field
"Armies of the Night"
Durst Lambda print on photographic paper. Original print 30 x 30 inches". 2000.

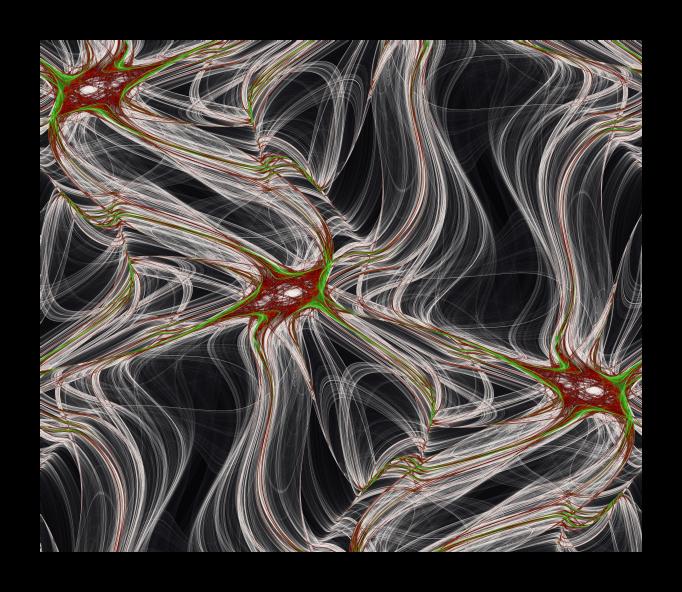
"Neueral Net"
Durst Lambda print on photographic paper. Original print 30 x 24 inches". 2002.
Mike Field is a mathematician from England who is professor of mathematics at the University of Houston, Texas. Before coming to Texas, he lived for about sixteen years in Sydney, Australia, and many of his pictures are strongly influenced by the light and colors of the Australian Outback. Michael Field's mathematical work lies on the boundary between the geometric theory of dynamical systems and ergodic theory. Much of his work has been in the area of dynamical systems symmetric with respect to a compact Lie group of transformations. More recently he has been working on problems in smooth ergodic theory, notably problems about the stability and rate of mixing for hyperbolic flows. In his pictures, he uses ideas based on his mathematical work as a way of expressing in an abstract way the underlying structure that lies within chaos and randomness.
"Symmetry imposes a unity and harmony on a design. The particular symmetry (and color) used in the design can also have a psychological and physiological impact on the viewer. Moreover, 2-color patterns often contain subtle optical illusions. My interests lie in exploring some of these relations. Unlike the classic static bathroom tile repeating pattern, many of the pictures I have worked on are quite unsettling in their shifting dynamics and colors - this is quite intentional, I am not very interested in "pretty pictures". An aspect of my art work that I particularly enjoy is that I write the software for all the programs I use as well as build the computers that run the software. In this sense, I like to feel that theory (mathematics), art (outcome), software (algorithms) and engineering (hardware) are integrated and that no one part survives without the others.
"Technically speaking, all of the images I create are realizations of invariant measures of symmetric chaotic dynamical systems. The coloring reflects the density of the invariant measure. ArmiesOfTheNight was created using a symmetric deterministic dynamical system defined on the two-dimensional torus. The resulting invariant measure was lifted to the plane so as to produce a repeating pattern of the plane. In fact, matters are a little more complicated... ArmiesOfTheNight is a 2-color repeating pattern. Half of the symmetries of the pattern preserve colors and half interchange colors. (In Coxeter's notation, the pattern is of type pm/cm.) A lot of the mathematical work that goes into the creation of these 2-color patterns relates to the development of algorithms that allow one to do the 2-coloring in a way consistent with the dynamics and symmetry of the pattern. By comparison, NeuralNet is a rather simple "1-color" pattern - except that in this case, only a part of a generating tile is shown. The underlying pattern is a repeating pattern of type pgg. Patterns of this type have no reflection symmetries. The absence of reflectional symmetries often leads to very fluid and dynamic patterns."
Email: mf@uh.edu or MikeField@gmail.com
Web: http://nothung.math.uh.edu/~mike or http://www.ma.ic.ac.uk/~mjfield
(I am presently a Visiting Leverhulme Professor of Mathematics at Imperial College London.)



