Nathan Selikoff
Freelance Artist
The Fine Art of Nathan Selikoff http://www.nathanselikoff.com/
Digital Awakening Studios | Graphic and Web Design Solutions
http://www.digitalawakeningstudios.com
nselikoff@gmail.com
"I love experimenting in the fuzzy overlap between art, mathematics, and programming. The computer is my canvas, and this is algorithmic artwork - a partnership mediated not by the brush or pencil but by the shared language of software. Seeking to extract and visualize the beauty that I glimpse beneath the surface of equations, I create custom interactive programs and use them to explore algorithms, and ultimately to generate artwork. In the world of chaotic dynamical systems, minute changes in initial conditions produce radically different results. The interface of my software gives me hooks into the algorithms and allows me to exert some control. Art and mathematics, the right brain and the left, are inextricably linked in this work. My art depends on mathematics, yet simultaneously illuminates and unravels its beauty. I am an explorer who uncovers something extraordinary, bringing into view that which was always there to be discovered."
“Helios [var. 1198505515] ”
2007, Lightjet Print, 24" x 24"
Underlying this artwork is a two-dimensional plot of the "typical behavior" of a chaotic dynamical system, a strange attractor. The base image is computed with a set of iterated functions, which serve as a numerical approximation to integrating the underlying differential equations. The iterated functions contain four coefficients, which are controlled by sliders in interactive custom software and control the appearance of the attractor. Once the particular form is chosen, it is rendered as a high-resolution 16-bit grayscale image, colorized using gradient mapping and edited to enhance contrast, control composition, and add special effects.
“SA_1188475827 ”
2007, Lightjet Print, 19" x 24"

Underlying this artwork is a two-dimensional plot of the "typical behavior" of a chaotic dynamical system, a strange attractor. The base image is computed with a set of iterated functions, which serve as a numerical approximation to integrating the underlying differential equations. The iterated functions contain four coefficients, which are controlled by sliders in interactive custom software and control the appearance of the attractor. Once the particular form is chosen, it is rendered as a high-resolution 16-bit grayscale image, colorized using gradient mapping and edited to enhance contrast, control composition, and add special effects.
“ SA_1188415571 ”
2007, Lightjet Print, 24" x 19"

Underlying this artwork is a two-dimensional plot of the "typical behavior" of a chaotic dynamical system, a strange attractor. The base image is computed with a set of iterated functions, which serve as a numerical approximation to integrating the underlying differential equations. The iterated functions contain four coefficients, which are controlled by sliders in interactive custom software and control the appearance of the attractor. Once the particular form is chosen, it is rendered as a high-resolution 16-bit grayscale image, colorized using gradient mapping and edited to enhance contrast, control composition, and add special effects.
“ Death Mask 2 ”
2007, Inkjet Print, 24" x 24"
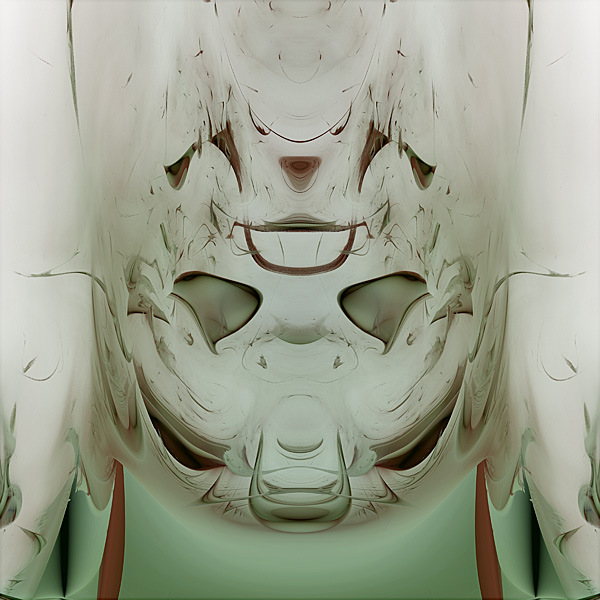
This artwork is a two-dimensional plot of the Lyapunov exponent of a chaotic dynamical system. The Lyapunov exponent is a measure of how chaotic the system is, and in this case, the system is a strange attractor with a four-dimensional phase space. Two of the dimensions are static, and the other two vary in the x and y directions of the image. A custom program renders four 16-bit grayscale images, which represent the different "components" of the spectrum of Lyapunov exponents. These images are combined in Photoshop using a pseudo-color technique to bring out subtle coloration in the final artwork.
“ Owl King ”
2007, Inkjet Print, 24" x 24"

This artwork is a two-dimensional plot of the Lyapunov exponent of a chaotic dynamical system. The Lyapunov exponent is a measure of how chaotic the system is, and in this case, the system is a strange attractor with a four-dimensional phase space. Two of the dimensions are static, and the other two vary in the x and y directions of the image. A custom program renders four 16-bit grayscale images, which represent the different "components" of the spectrum of Lyapunov exponents. These images are combined in Photoshop using a pseudo-color technique to bring out subtle coloration in the final artwork.