Robert Fathauer

"Iterated Lattice No. 1"

Digital print, 8" X 24", 2007.

This print was created by stylizing a seven-crossing knot and then iterating it. The starting geometric shape is a regular hexagon, shown at the top of the print. Below it is the stylized knot. Below that is the first iteration, in which four smaller copies of the knot are added. At the bottom of the print is the second iteration, in which four even smaller copies are added to each of the four small copies found in the first iteration. This process could be continued ad infinitum with the knot remaining unicursal (a single strand). The print contains a single strand that weaves through the four stages in alternating over/under fashion. The esthetics of the design are intentionally borrowed from Islamic lattice designs.

"Infinity"

Digital print, 12" X 12", 2006.




This print is based on a unicursal fractal knot. The starting point is a particular projection of the trefoil knot. The knot is then iterated by incorporating two smaller copies within loops in the starting knot in such a way that the resulting more complex knot remains unicursal. Additional iterations using the same algorithm yield a fractal knot.

"Square Knots Stretching to Infinity"

Digital print, 14" X 14", 2007.



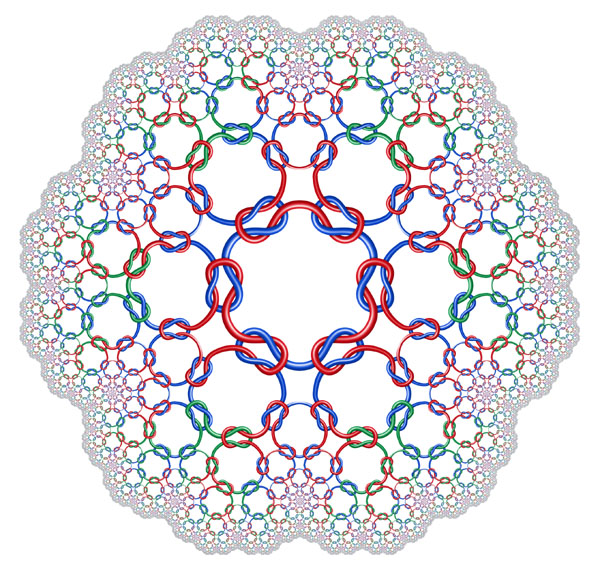
This print depicts a fractal link design. Each strand has four lobes and connects to other strands via square knots. The design was created by decorating the individual tiles in a fractal tiling with knot-like graphics