Daniel Erdely, Walt van Ballegooijen, Marc Pelletier and the Spidron Team

"Spidronized Archimedean Solids"

Series of 13 pieces of #3D print, 12 cm X 12 cm X 12 cm, 2006.



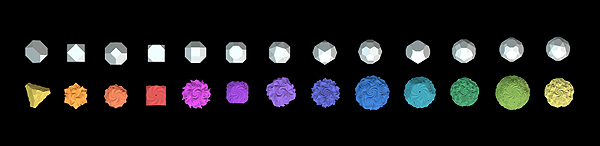
Transforming the classical Archimedean solids we found a new way of artistic expression and new geometrical objects with interesting properies. As all of the shapes can be constructed from planar polygons and representing artistic potential, they can be good tools of education and recreation.

"Spidronized Platonic Solids"

Series of 5 pieces of 3D print, 12cm X 12cm X 12cm, 2006.




Transforming the classical Platonic solids we found a new way of artistic expression and new geometrical objects with interesting properties. As all of the shape can be constructed from planar polygons and representing artistic potential, they can be good tools of education and recreation. Some of them are spacefillers, like spidro-octahedron and spidro-tetrahedron, which is quite interesting as the original platonics are not.

"Dodeca Spidroball Lampshader"

Paper , 45cm X 45cm X 45cm, 2006.



Among the Spidronized Platonics this dodecahedral shell seemed to be the most attractive. Maybe this property helped it to the cover of Science News in October 2006. In this issue there is a longer articles on Spidrons, written by the well kown scientific journalist, Ivars Peterson.

"Non-periodical Spatial Labyrinth"

Paper , (Freely can be composed from dodecagons, in situ), 2006.



This work of art was invented by Marc Pelletier during the developement of the Spidron project. We have Spidron gatherings every year in the Netherlands, where during the experiments we realised that adjusting the centers of the spidron nests to the middlepoints of Obtuse and Acute rhombohedra we can create very interesting and continous spatial labyrinths, which are, like the A6-O6 system, also non-periodical. The shadows of these complex compositions are corresponding to the Kepler titilngs.

Daniel Erdely, freelance artist and PhD studient in Cultural Studies, Pecs, Hungary, and Walt van Ballegooijen, Marc Pelletier and the Spidron Team Spidron Bt. Budapest, Hungary

http://www.spidron.hu

"As a longer process the spidron project is going on for years. In the last 4 years significant development was taking place.With my colleagues, Walt van Ballegooijen, Marc Pelletier, Amina Buhler-Allen, Rinus Roelofs, Lajos Szilassi and Paul Gailiunas we created a series of never seen geometrical shapes based on the basic spidron idea. Among them, the most significant are the "spidronized" Platonic and Archimedean solids, Penrose tilings and the non-periodical spatial labyrinths."